
University of California, Irvine
Instructor: Dr. Barbara J. Becker

|
|
|
|
|
| Before the Copernican system could be accepted as more than a mathematical
convenience,
a new physics would have to be developed to explain the "natural" motions of things. In the old Aristotelian physics:
|
Pre-paradigm phase
|
|
|

Each star in René Descartes' universe is surrounded by a swirling vortex of matter. Planets do not possess their own independent motion, but are simply carried around their sun with the rest of the vortex matter. In this way, Descartes could agree with the general structure of the Copernican system and still argue that the earth does not move relative to its surroundings. |

René Descartes (1596-1650) |
As a young boy, Descartes received an excellent
education. His lessons came from textbooks based on the writings
of the ancient Greeks. Young René quickly mastered the mathematics
of Euclid, the physics of Aristotle, and the anatomy of Galen. The
more he learned, the more he wanted to know. The more he knew, the
more questions he asked. He wondered, for example, how Aristotle
could be so sure that the earth was at rest in the middle of the universe
while the mathematician Copernicus was equally certain that the earth was
in motion around the sun. Aristotle had reached his conclusions by
relying on his senses. Copernicus had reached his conclusions by
relying on mathematics.
Who was right?
|
| While looking for answers to such
puzzling questions, Descartes became distrustful of the knowledge he had
learned in school. He gave up reading all books and set out on his
own personal search for truth. His search was adventurous and exhausting.
For several years, he served as a volunteer soldier and travelled throughout
Europe. But at the age of 25, he gave up the soldier's life and settled
in Holland where he devoted himself to the study of mathematics and philosophy.
René Descartes made many important contributions to mathematics and science. He derived a mathematical expression to describe the bending (refraction) of light as it travels through different transparent materials. He introduced the use of exponents to mathematics. Anyone who has ever plotted points on a graph using an algebraic formula owes Descartes a debt of gratitude. Perhaps his greatest achievement was his creation of an entirely new method of scientific investigation, a method which he proposed as a replacement for that of the ancients. Descartes was convinced that humans can gain certain knowledge of the world and how it works, but only if they build that knowledge on a firm foundation of simple and indisputable truths. Ordinarily, Descartes argued, our minds are cluttered by the distracting and deceptive information that bombards our senses every day. That is why these simple and indisputable truths have remained inaccessible to our understanding. Putting his own method to work, Descartes cleared his mind of all preconceptions. Starting from scratch, he constructed an entirely new system of the world--a world composed only of matter and motion. The complexity of the observable world is only an illusion, he claimed. In reality, everything we humans sense is the product of innumerable collisions between extremely small particles of matter. These collisions are controlled by two basic ideas:
|
|
| Christiaan Huyghens was only about 15 years old
when he first encountered the ideas of Descartes. He was enthused
by much of what he read. Still, there were times when the French
philosopher's words just didn't seem to make any sense at all. For
a while, the young scholar blamed his inability to fully understand Descartes'
system of the world on his own ignorance. But gradually, he began
to realize that the problem lay in Descartes, not in himself. Huygens
became determined to correct Descartes' errors.
Huyghens did not share Descartes' extreme skepticism about the value of experimental results. Human senses may be faulty, he admitted, but they are not totally unreliable. |

Christiaan Huyghens (1625-1695) |
With adequate care and repetition of controlled scenarios, Huyghens was confident the limitations inherent in human sensory perception could be reduced. He knew from experience that human senses could be artificially extended through the use of instruments. At the age of 26, Huyghens designed and built an excellent telescope with which he discovered the ring of Saturn as well as its moon Titan, the first moon of that planet to be identified. At the age of 27, he designed and built an accurate clock. By introducing this new instrument into the investigator's toolkit, Huyghens revolutionized the study of moving bodies. His pendulum-driven timepiece allowed him to make more precise measures in free-fall experiments than any of his predecessors. For Huyghens, using experimentation hand-in-hand with reason proved a winning combination throughout his life. His methodical study of colliding bodies led him to reject Descartes' ideas on collision and propose a very different set of rules governing their behavior. |
|
|
|
|
|
|
|
Two equal bodies move toward each other at equal speeds. |
|
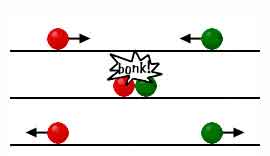 They will be reflected and continue to move at equal speeds. |
 They will be reflected and continue to move at equal speeds. |
|
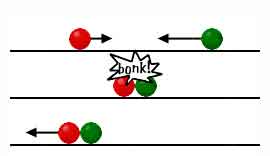
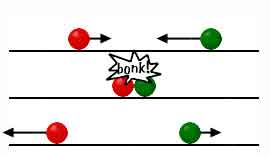
Two equal bodies move toward one other at different speeds. |
|
 The slower one will be reflected. Both bodies will continue to move in the direction of the faster one with a speed that is the average of the two. |
 They will move with their speeds reciprocally exchanged. |
|
One body moves toward another equal body that is at rest. |
|
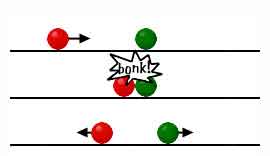 The moving body will give some of its speed to the one at rest, and will be reflected back with the larger share of that speed. |
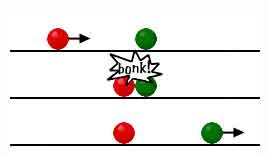 The moving body will stop while the one that had been at rest will move forward with the same speed as the body which struck it. |
|
One body moves toward a slightly bigger body that is at rest. |
|
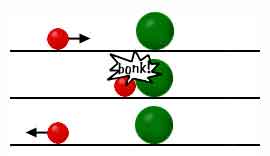 No matter how fast the moving body is going, the body at rest will not be moved at all while the one in motion will be reflected. |
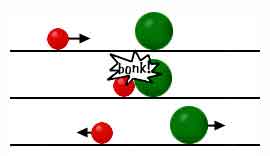 No matter how slowly the moving body is going, the body at rest will be moved. |
|
|
| According to René Descartes (ca. 1630): |
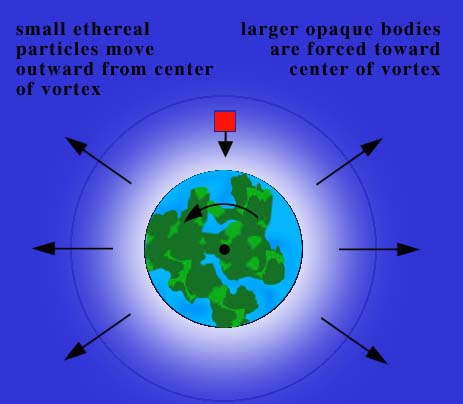 |
| According to Isaac Newton (ca. 1664-1675): |
 |
![]()
![]()
![]()
|
|
First of the Age of Reason?
A calculus fit to compute on,
--Gina Berkeley
Nature and Nature's laws lay hid in night:
--Alexander Pope (1688-1744) |
|
|
|
|
born at Grantham |
|
|
enrolled at Trinity College, Cambridge |
|
|
Anni Mirabiles (Remarkable Years)
|
|
|
"New Theory about Light and Colors" published in Philosophical Transactions |
|
|
Edmund Halley visited Isaac Newton to discuss the question of why planetary orbits are elliptical |
|
|
composed Principia |
|
|
Philosophiae Naturalis Principia Mathematica [Mathematical Principles of Natural Philosophy] published |
|
|
appointed Warden of the Mint |
|
|
appointed Master of the Mint |
|
|
elected to Parliament |
|
|
elected President of the Royal Society |
|
|
published Opticks |
|
|
published second edition of Principia |
|
|
published third edition of Principia |
|
|
died at London; buried in Westminster Abbey |
Young Newton's Guides to Conducting Experiments |
Francis Bacon, Novum Organum (1620): Suppose you are curious about the true nature of some phenomenon. Take heat, for example. How would you begin to investigate it? |
|
René Descartes, Rules for Philosophizing (c. 1628):
|
![]()
![]()
![]()
|