Conservation and Collisions

Speed describes the rate at which a body changes its position. Velocity provides information about its direction of travel as well.  But sometimes speed and velocity aren't enough to tell you all you need to know about a body's "quantity of motion."

Suppose you are alerted that a body, 1 km away, is traveling directly toward you at 5 km/hr.  Armed with that information, you can predict that the body will reach you in 12 minutes.  Being able to calculate the body's expected time of arrival may give you some small sense of control over the situation, but it would be even more helpful to know if the body in question is mosquito-sized or elephantine.  When moving bodies interact, the outcome depends on more than just their rate of travel.

Momentum is a convenient way of describing a body's motion that takes into account how much stuff is in the body (its mass), how fast it is going, and in what direction (its velocity).  Momentum is represented mathematically with the simple statement:

When we notice a body speeding up, slowing down, or altering its direction of travel, we say that it has changed its momentum because a force is acting on it.  Even though we may not know what kind of force it is (mechanical, gravitational, electrical...), we can still determine its strength by observing the amount of change in momentum it caused:

=  force.

It seems trivial to say that if there is no force acting on a body, it will experience no change in its momentum.  Like, duh!  But Isaac Newton pointed out that this is also true for a system of mutually interacting bodies.  The total momentum of such a system at any given instant is simply the sum of the momenta of all its individual components.  If we examine the system a second later, we may discover that one individual component in the system has lost some of its original momentum, but its loss will be the others' gain.  As long as there is no outside force acting on the system as a whole, its total momentum will remain the same:

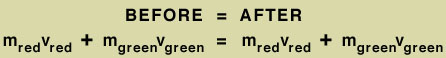
This fundamental principle is called the conservation of momentum.  Recognizing that momentum is conserved in all collisions was an important step forward in understanding the physics of interacting bodies.

Let's use some hypothetical values for the mass and velocity of two balls before and after they collide so we can tally up the total change in momentum that occurs in each of the following collisions.

MOMENTUM		BEFORE				AFTER				TOTAL
Collision I
	red	2	1	2		2	-1	-2
	green	2	-1	-2		2	1	2
				0				0		0
Collision II
	red	2	1	2		2	-2	-4
	green	2	-2	-4		2	1	2
				-2				-2		0
Collision III
	red	2	1	2		2	0	0
	green	2	0	0		2	1	2
				2				2		0
Collision IV
	red	2	1	2		2
	green	4	0	0		4
				2						0

Collision III is an interesting case.  After the moving red ball strikes the stationary green ball, it comes to an abrupt halt while the green ball begins to move.  Is this a special case?  Would the outcome be different if we doubled the balls' masses, or tripled the red ball's original velocity?

Repeated trials show that whenever a stationary ball is hit head-on by another one just like it, all the motion of the moving ball is always transferred to the target ball, regardless of the moving ball's speed.  There is nothing in the law of conservation of momentum that requires this outcome.

NOTE:  Momentum does a fine job of describing what has happened.  This is the job that Isaac Newton intended it to do.  Gottfried Wilhelm Leibniz, on the other hand, argued that momentum alone is insufficient to describe everything that is interesting and useful about the motion of colliding bodies.  In Leibniz's view, there must be yet another way to talk about motion that will provide insight into the why as well as the what of collision outcomes.  This is what came to be known as vis viva.

Expressed this way, vis viva bears a strong resemblance to what we call kinetic energy, or energy of motion:

kinetic energy =

Once again, let's use some hypothetical values for the mass and velocity of each ball before and after each collision, so we can tally up the total change in kinetic energy that occurred:

KINETIC ENERGY		BEFORE				AFTER				TOTAL
Collision I
	red	2	1	1		2	-1	1
	green	2	-1	1		2	1	1
				2				2		0
Collision II
	red	2	1	1		2	-2	4
	green	2	-2	4		2	1	1
				5				5		0
Collision III
	red	2	1	1		2	0	0
	green	2	0	0		2	1	1
				1				1		0
Collision IV
	red	2	1	1		2
	green	4	0	0		4
				1						0

Like momentum, kinetic energy is conserved in each of these collisions:

An elastic collision is one in which all the kinetic energy the colliding bodies possess (that is, energy due solely to their motion), is the same before, during, and after the collision takes place.  Another way to say this is that an elastic collision is one in which kinetic energy is conserved:

NOTE:  In reality, there are no truly elastic collisions.  They exist only in that deliciously strange land--the world of abstract ideas--where such fabulous things as frictionless pulleys, true vacuums, and imaginary numbers reside.  The idea of an elastic collision is an invention, a tool, a useful construct that mathematicians and scientists use to keep tabs on change in the universe.

Lost???!!!  Is this sort of thing even legal??  What about all those conservation laws???  With such strict rules governing the behavior of things in the universe, where can lost kinetic energy go?

This brings us to the matter of inelastic collisions in which some or all energy of motion is lost, that is, all real collisions.  Inelastic collisions posed a difficult problem for proponents of vis viva. Vis viva was not supposed to be created or destroyed no matter what happened.

Compare the outcomes of the inelastic collisions shown below with those of the elastic collisions we've just discussed:

Kinetic Energy in Inelastic Collisions		BEFORE				AFTER				TOTAL
Collision I
	red	2	1	1		2	0	0
	green	2	-1	1		2	0	0
				2				0		-2 (100% loss)
Collision II
	red	2	1	1		2
	green	2	-2	4		2
				5						(90% loss)
Collision III
	red	2	1	1		2
	green	2	0	0		2
				1						(50% loss)
Collision IV
	red	2	1	1		2
	green	4	0	0		4
				2						(83.3% loss)

Yikes!  In every case, the kinetic energy after the collision, is less than it was before.  Look at Collision I!  How can two bodies (supposedly possessing lots of vis viva because of their mass and velocity) suddenly stop dead in their tracks after they collide?  Where does their motion go?  What happens to their vis viva?

Does this mean the Law of Conservation of Energy is invalid?  No.  Energy is the common currency of exchange for all the different forces that push and pull on objects in our world.  It exists in many forms:

Mechanical energy can be used to lift a bowling ball from the floor up to a closet shelf.  As the ball is lifted, work is done against the force of gravity.  Once the ball is on the shelf, the energy that has been used is stored as potential energy.  If the shelf breaks a second later--or a minute, a day, or even a thousand years later--the bowling ball will fall back to the floor.  The stored gravitational energy will be converted into energy of motion as the ball falls, into sound energy as it smacks the floor, into heat energy as the molecules in the floor and ball and surrounding air are set into vibration, into mechanical energy as the floor is splintered, and even into electrical energy if the bowling ball happens to move a generator as it falls.  The amount of energy in the system remains the same, but it may take some careful analysis to account for every last erg.

Now, let's see what happens to the momentum of the red and green ball after each inelastic collision:

Momentum in Inelastic Collisions		BEFORE				AFTER				TOTAL
Collision I
	red	2	1	2		2	0	0
	green	2	-1	-2		2	0	0
				0				0		0
Collision II
	red	2	1	2		2		-1
	green	2	-2	-4		2		-1
				-2				-2		0
Collision III
	red	2	1	2		2		1
	green	2	0	0		2		1
				2				2		0
Collision IV
	red	2	1	2		2
	green	4	0	0		4
				2						0

Even though the velocities of the red and green ball have been reduced in the aftermath of the inelastic collisions, momentum is still conserved!  This demonstrates the power and utility of the Law of Conservation of Momentum in analyzing complex physical interactions.

Go to: History 60 Home Page Weekly Readings 1 2 3 4 5 6 7 8 9 10 Lecture Notes 1 3 5 7 9 11 13 15 17 19 2 4 6 8 10 12 14 16 18 20 Quodlibets 1 2 3 4 -- 5 6 7 8 --