HISTORY 135C

HISTORY 135C

Department of History
University of California, Irvine
Instructor: Dr. Barbara J. Becker
![]()
Lecture 9. The Clockwork Universe.
![]()
A New Physics for a New (Heliocentric) World |
Before the Copernican system could be accepted as more than a mathematical convenience, a new physics had to be developed to explain the "natural" motions of things. Aristotelian physics:
If Earth is not The Center, or if there are multiple centers -- then what? How can natural motion be explained?? If Earth is a celestial body, is there really a difference between terrestrial motion and celestial physics? What should "Copernican" physics be like? |
René Descartes (1596-1650) |
|

|
Around 1660, a young Cambridge University student named Roger North reacted to the views of French philosopher, René Descartes: As to study there, I followed my own appetite, which was to natural philosophy, which they call physics, and particularly D. Cartes, whose works, I dare say, I read over 3 times before I understood him. And at that time new philosophy was a sort of heresy, and my brother could not encourage me much in it.... |
But I found such a stir about Des Cartes, some railing at him, and forbidding the reading him, as if he had impugned the very Gospel and yet there was a general inclination, especially of the brisk part of the university, to use him, which made me conclude, there was something extraordinary in him.... |
|
Descartes' World |
|
Maybe all motion, terrestrial and celestial, is forced motion of one sort or another. "Space" in the universe is completely filled with fine celestial matter. The only way for something to move is if it pushes something else out of the way. |
|
|
|
|
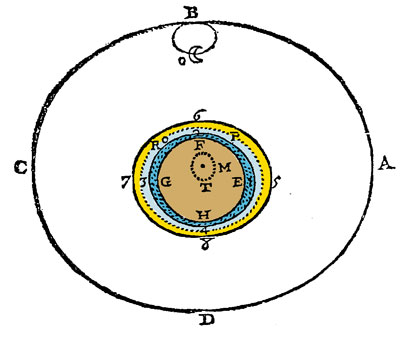 An imaginary planet (T) -- a lot like Earth -- is surrounded by layers of water and air. |
|
|
|
|
According to Descartes, all celestial motion can be explained on the basis of this simple vortex model. |
|
According to Descartes, all terrestrial motion can be explained by the vortex model, too.
As the fine celestial matter is whisked outward by the vortex's whirling motion, larger, more massive bodies move downward toward the vortex's center to fill the empty spaces left behind. |
|
Giambattista Riccioli (1598-1671) |
Not everyone was ready to move into the heliocentric camp. In 1651, renowned Jesuit astronomer, Giambattista Riccioli (1598-1671) published Almagestum Novum (The New Almagest) in which he listed 20 arguments in favor of the Earth's motion and 77 against it! His book appeared with the following frontispiece:
In the illustration, Astraea (goddess of justice) puts the heavenly spheres to the test with her trusty scales. Ptolemy's system has already been weighed and found wanting. A sphere representing his geocentric universe lies discarded on the ground in the lower right hand corner. Meanwhile, Ptolemy (seated on the ground) himself looks on approvingly as the lightweight system of Copernicus (depicted as the sphere on the left) is outweighed by that of Riccioli himself. Riccioli's universe resembles Tycho's geo-heliocentric system in many respects. Unlike Tycho, Riccioli contended that only Mercury, Venus and Mars orbit the Sun. The Sun, Jupiter and Saturn orbit the stationary Earth. |
Isaac Newton (1642-1727) |
|
|
Then ye who now on heavenly nectar fare,
Edmund Halley Preface, Philosophiae Naturalis Principia Mathematica |
|
|
|
|
born at Grantham in northern England | |
|
|
enrolled at Trinity College, Cambridge |
|
|
|
recorded naked-eye observations of a comet in his Waste Book, or journal, under a section headed "Quaestiones quaedam Philosophicae" (Certain Philosophical Questions) set aside for his musings on natural phenomena (heat, light, sound...) bought and read books on mathematics and astronomy including Galileo's Dialogue on the Two Chief World Systems and Descartes' numerous philosophical works, most notably the Principia Philosophiae learned about Kepler's "first" and "third" laws of planetary motion from Thomas Streete's new book, Astronomia Carolina (1661) recorded his early views on the nature of "Gravity and Levity" in the Quaestiones:
Newton's early thoughts on the nature of gravitational attraction are reminiscent of Descartes' vortical theory. |
|
In Newton's view of gravity, ethereal matter is contantly rising. When it reaches the upper atmosphere it condenses and begins to "rain down" on the Earth. As it falls, it presses down on all substantive matter. |
||
Newton analysed the circular motion of a ball on a string. Armed with Descartes' law of inertia, he focused his thoughts on the ball and its resistance to change in either its rate or direction of motion. Constrained by the string to move in a circle, the whirling ball is constantly being forced to change its direction. At every instant, because of its natural tendency to move forward without constraint, the ball resists that change. Newton referred to this resistance as "centrifugal endeavor", a calculatable quantity (= v2/r, where "v" is the speed of the ball and "r" is the length of the string). August. With a deadly outbreak of bubonic plague spreading through England, Cambridge University sent students home as a precaution. Students were invited to return the following March, but a resurgence of the epidemic sent them home again in June. Classes did not resume until spring 1667. |
||
Newton spent the duration of Cambridge's hiatus at his home, Woolsthorpe, in Grantham. While there he applied what he had learned about the motion of a ball on a string to the problem of planetary orbital motion (assumed here to be circular). The situations are similar, but not precisely identical:
When Newton calculated the "centrifugal endeavor" of each planet and compared their values, he found them to be proportional to 1/r2, where "r" is a given planet's distance from the Sun. Note that Newton is merely describing the planets' inertial response to an external constraint on their motion. He has not characterized the force at work. That is because he still thought of planetary motion in a very Cartesian way: Planets are swept along by the swirling solar vortex. Indeed, he continued to think about planetary motion in those terms for many years. That is not the way Newton's views on planetary motion are commonly presented in historical accounts. According to biographers who knew Newton personally in his later years, the young scholar was "pensively meandering" in the garden at Woolsthorpe one day when a falling apple caught his attention. He is reported to have wondered if the force that pulled the apple to the ground extended as far as the Moon. Could this be the same force that keeps the Moon tethered in its orbit around the Earth? How strong would that force be at such a great distance?
An apple tree in the garden outside Newton's apartment at Trinity College, Cambridge as seen in May 2009. The tree has been grown from a graft of an apple tree reputed to have been "the" tree whose falling apple inspired Newton to ponder the relative strengths of Earth's gravitational pull on the apple and the Moon. These accounts are based on Isaac Newton's own recollections of events. It is tempting to give great weight to such an authoritative eyewitness, but it is important to keep in mind that Newton was describing his earliest thoughts on the question of gravity long after Principia had been published, read and acclaimed. There is no contemporaneous evidence to verify that Newton was even thinking about gravity as an attractive force at this early stage in his career. Hindsight always colors even the best of memories. Priority disputes -- such as the one that Newton became embroiled in with Robert Hooke over who was the first to enunciate gravity's inverse-square law -- further skew participants' memories of what they did and when they did it. |
||
|
1668
|
created his first working model of a reflecting telescope
|
|
1675
|
Newton infused his ethereal gravity with an active principle lacking in Descartes' passive mechanical scheme. The subtle and fluid ether that fills all the pores of matter in Newton's universe nourishes and sustains not just the Earth, but the Sun and other bodies in it.
|
correspondence with Robert Hooke prompted Newton to think more deeply about the nature and cause of free fall and of planetary motions began to describe such motions, not in terms of a moving body's inertia, but as a natural and dynamic response to a center-seeking attractive force |
|
| wrote a paper on comets which still seems to be based on an assumption that bodies in the solar system move in Cartesian vortices | |
|
|
January. Christopher Wren (1632-1723), Robert Hooke (1635-1703) and Edmund Halley (1656-1742) met in a coffeeshop. The conversation turned to an interesting puzzle: what shape would planetary orbits have "supposing the force of attraction towards the Sun to be recipocal to the square of their distances from it"? Recall that as early as 1603, Kepler had declared all planetary orbits to be elliptical. But this was a conclusion based on observational evidence. An ellipse was the best fit Kepler could find to match Tycho's data. What if you tackled the problem the other way around and started from unassailable mathematical principles? Would you get the same answer? Hooke was certain that orbital paths must be ellipses and claimed he could demonstrate it mathematically. Wren offered a prize to the first of the three who brought in a proof for all to see. August. Months passed and Hooke had yet to produce his evidence. Edmund Halley traveled to Cambridge to find out what Isaac Newton had to say on the matter. When Halley put the question to Newton, Newton promptly replied, "It would be an Ellipsis." When Halley asked Newton how he could be so sure, Newton replied "Why ... I have calculated it." November. Newton sent Halley a nine-page manuscript titled De Motu Corporum in Gyrum (On the Motion of Orbiting Bodies).
In De Motu, Newton finally abandoned all remnants of the Cartesian vortical system and turned instead to one in which a planet's orbital motion is governed by a Sun-centered attractive force that decreases in strength with the square of the planet's distance from the Sun. |
|
|
prodded and cajoled by Halley, Newton slowly but surely constructed a more complete presentation of his views on motion upon the foundation he had established in De Motu |
|
|
Philosophiae Naturalis Principia Mathematica [Mathematical Principles of Natural Philosophy] published with Halley's financial assistance
|
Newton developed a new and revolutionary view of falling bodies -- a view that brought the physics of the terrestrial and celestial realms together into one simple package.
All bodies, regardless of size, shape, constitution, color, texture.... generate and respond to gravitational forces in the same way. The Earth pulls on and is pulled by an apple (a terrestrial body) in the same way it influences and is influenced by the Moon (a celestial body). Although it took a while for Newton's ideas to become known, understood, and accepted, the days of the Earth-centered universe were numbered. As perfect circles gave way to ellipses and the distinction between terrestrial and celestial matter evaporated, Aristotle's physics became more and more of a philosophical fossil: a relic from which students could learn "what people used to think." |
Notable Events in Newton's Life (cont'd) |
|
|
|
appointed Warden of the Mint |
|
|
appointed Master of the Mint |
|
|
elected to Parliament |
|
|
elected President of the Royal Society |
|
|
published Opticks |
|
|
published second edition of Principia |
|
|
published third edition of Principia |
|
|
died at London; buried in Westminster Abbey
|
|