Lecture 2

HISTORY 135C

Department of History
University of California, Irvine
Instructor: Dr. Barbara J. Becker

Lecture 2. From Chaos to Cosmos.

Early Sky Watchers -- The Greeks

The Greek world in the 5th and 4th centuries BCE.

__________

First Principles

To account for		which the Greeks called...
stability in the world...	find what is fundamental, constant and unchanging...	arché
diversity in the world...	find what is different, what changes, and how it changes; this will reveal the rules or agencies that control the change process...	physis
pattern in the world...	use these rules to organize the fundamentals into a "neat array"...	cosmos

Plato (429-348 BCE)


	Plato as the young pupil of Socrates

Two worlds:

Real world	Ideal world
always in flux	always constant
knowledge obtained directly through the senses	knowledge revealed by jogging memories already in the soul
result: a likely story	result: truth

Mathematics (geometry) bridges these two worlds and makes the Ideal world accessible to human understanding through reason.

Plato's Ideal Educational Plan


"No one may enter here [The Academy] who is ignorant of mathematics."--Plato

Quadrivium
(subjects comprising the necessary education for all citizens and civic leaders)

Arithmetic

Geometry

Music

Astronomy

number

number in space

number in time

number in motion

Plato's "Likely Story" about the Structure and Substance of the Natural World

The Timaeus

Plato's Views on Time and the Heavens

Time came into being with the heavens.... As a result of this plan and purpose..., the sun and moon and the five planets ... came into being to define and preserve the measures of time.
--Plato, Timaeus

The earliest clocks and calendars were based on the natural rhythms of the Sun and the Moon. But what kind of time units can we measure using planetary motions? Can we identify cyclic patterns in the wanderings of the planets that can serve as markers for other useful units of time? How can the apparent complexity of planetary motions be described mathematically?

The photographs below were taken during the conjunction of Venus, Mars, and Jupiter in June 1991. (Planets are said to be in conjunction when they share the same celestial longitude.) All three of these planets are moving against the background stars, but to simplify the complexities of their motion, I have fixed the position of Mars in each frame (it is the faint "star" in the upper left-hand corner).

Venus (the brightest of the three bodies) can be seen moving up toward Mars (upper left in the first frame). In the final frame, Venus has passed to the left of Mars. Jupiter, meanwhile, moves down toward the bottom right hand corner. In the final frame, the three planets form nearly a straight line with Venus in the upper left corner, Jupiter in the lower right corner, and Mars between them.

	June 16
	June 17
	June 18
	June 20
	June 22
	June 25

Eudoxus of Cnidus (c. 400 - c. 347 BCE)

Eudoxus, a student of Plato, developed an ingenious mathematical system to bring some order to the complexities of planetary motion.

Eudoxus treated each celestial body as a separate mathematical problem, but he tackled each of these problems in the same way. In his system, the motion of each planet (Mercury, Venus, Mars, Jupiter, and Saturn) is governed by a set of four nested concentric spheres -- one to govern its daily motion, one to govern its motion through the zodiac, and two to account for the looping appearance of its retrograde motion. The Sun and Moon were governed by three spheres each.

Simplified schematic of Eudoxus's concentric sphere model. The Earth (blue) sits in the center of the nested spheres that control the motion of the planet (red). The planet is shown embedded in a tilted sphere that carries it around the zodiac. This sphere is nested in a sphere that rotates daily on the polar axis of the fixed stars.

When all four spheres start rotating on their axes, the planet will appear to move along a complex path that resembles its observed motion across the sky.

Eudoxus's model worked pretty well for Jupiter, Saturn, and Mercury, and less well for Venus and Mars. His younger contemporaries, like Callippus of Cyzicus and Aristotle, tried to improve the system's match with reality by adding more spheres.

Aristotle (384-322 BCE)

Aristotle, like Eudoxus, was a student of Plato. And, like all good students, he was critical of his teacher's ideas.

Aristotle agreed that mathematics could serve as a model for good reasoning, but he questioned whether it was truly the sole path to scientific knowledge about the natural world. He acknowledged that mathematics is useful for gaining certain knowledge of the heavens, optics and perspective, but he found it to be limited when it comes to investigating many other natural phenomena. Living things, for example, do not adhere to rigid patterns of behavior. They require a new kind of reasoning, one based on what is probable, not just on what is certain. Aristotle regarded such probability-based reasoning as equally worthy a tool for the natural philosopher as reasoning that is based on mathematics.

__________

Fundamentals of Aristotle's Natural Philosophy

All matter is made of two parts:

hyle (HOO-lee) -- basic fundamental stuff
qualities -- characteristics (wet vs. dry; cold vs. warm) superimposed on hyle

The tension and balance generated by opposing qualities is behind all change observed in terrestrial world.

Aristotle's Physics of the Terrestrial Realm

Terrestrial Elements	Qualities
Earth	Cold and Dry
Water	Cold and Wet
Air	Warm and Wet
Fire	Warm and Dry

Each terrestrial element (earth, water, air, fire) has a natural place or state.

some amount of each element is present in every body

therefore, opposing qualities are always at work

if a body (animate or inanimate) is removed from the natural place or state of its predominant element (violent change), it will naturally strive to return where it belongs (natural change)

if a body's natural qualities become imbalanced (violent change), it will naturally seek a more suitable place or state for itself given its new nature (natural change)

Aristotle's Physics of the Celestial Realm

Celestial Element	Qualities
Quintessence, or aether	none

The celestial element (quintessence) has no opposing qualities.

quintessence is perfect and immutable

a celestial body moves forever according to its perfect nature in a perfect circle at constant speed

any sensory evidence to the contrary is illusory

Hellenistic Period (323-31 BCE)

Aristotle was the tutor of Alexander the Great (356-323 BCE). After Alexander's death:

Greek language and culture spread throughout the known world

Commerce became international

Greek learning influenced by contact with Babylonian science

Museum established in Alexandria

intellectual center of known world
literature, mathematics, astronomy, medicine
library containing over 400,000 scrolls


The Alexandrians (Hellenistic Period -- Greek influence)
Euclid	330-260 BCE	Mathematics • wrote The Elements
Aristarchos	310-230	Astronomy • estimated size of Moon relative to Earth (see below)
Archimedes	287-212	Engineering
Eratosthenes	276-195	Math/Astronomy • librarian at Alexandrian Museum • measured size of Earth (see below)
Hipparchus	190-120	Astronomy • mapped the heavens • studied Babylonian records • discovered Earth's precession

Aristarchos (c. 310 - c. 230 BCE) Measures the Moon

Lunar eclipse, July 5-6, 1982

By measuring the amount of time it takes for the Moon to enter the Earth's shadow (about 1 hr) and then to cross the Earth's shadow (about 3 hours) during a lunar eclipse, Aristarchos was able to estimate that the Moon is about one-third the size of the Earth.

The July 1982 lunar eclipse (featured in the photo above) was very well centered. The Moon's path cut almost diametrically across the Earth's shadow giving observers an excellent opportunity to estimate the Moon's size relative to Earth's.

During that eclipse, the Moon took 65 min to enter the umbra and 2 hr 51 min (= 171 min) to cross it. Using these values, we can calculate that the Moon's diameter is roughly 65/171, or 38% of the Earth's.

Aristarchos could not determine the absolute size of the Moon because no one had yet figured out a way to measure the size of the Earth! Also, Aristarchos knew that shadows of spheres are conical in shape, but he had no way to know how far away the Moon is when it cuts through Earth's shadow. To find out how much this affected his estimate, compare the size of the Earth and Moon using modern measures.

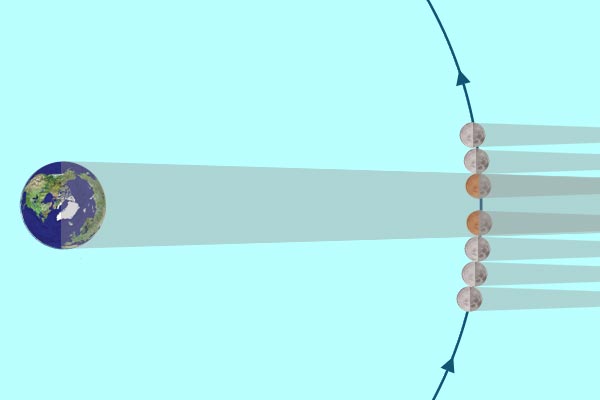
The Moon passing through the Earth's shadow during a lunar eclipse like the one in July 1982.

Eratosthenes (c. 276 - c. 195 BCE) Measures the Earth

The world of Eratosthenes showing the location of the cities of Alexandria and Syene.
________________

Eratosthanes lived and worked in Alexandria. The city of Syene is located due south of Alexandria at a distance of 5000 Greek stades. In Syene, there is a very deep well. Eratosthenes had heard that very year on the day of the summer solstice, when the Sun is directly overhead at noon, a brilliant shaft of sunlight illuminates the water at the bottom of this well.

________________

Meanwhile, back in Alexandria, Eratosthenes observed and measured the length of a shadow cast at noon by the summer solstice Sun. Using geometry, he determined that the distance between Alexandria and Syene was one-fiftieth of the Earth's circumference.

What was the size of Eratosthenes' Earth?

Two thousand years later, French astronomers Pierre Méchain and Jean-Baptiste Delambre set out to measure the Earth using modern methods. Their goal was to determine with precision and accuracy the distance between the Earth's north pole and its equator. By dividing that great distance into ten million equal parts, the savants -- in the name of the people of France and the good of all mankind -- created a new and natural standard of measure: the meter.

Eratosthenes' measure of the Earth's circumference was quite close to modern values.

How long, then, is a Greek stade in meters?

How far was Syene from Alexandria in modern measures.

What modern city is located on the site of old Syene?

If Eratosthenes and other learned individuals in the distant past knew the Earth was spherical, what's the big deal with Christopher Columbus?

The Alexandrians (Roman Empire -- Greeks living in Alexandria)
Hero	fl. 62 CE	Optics • studied reflection and refraction • constructed automated gadgets
Ptolemy	fl. 125	Astronomy/Cartography • wrote Almagest; The Geography
Galen	131-201	Medicine • wrote On the Natural Faculties

Claudius Ptolemy (c. 125 CE)

Ptolemy was a Roman citizen of Greek descent who pursued his mathematical interests at the great Museum in Alexandria, Egypt.

made important contributions to cartography, optics and other studies

sought to establish a mathematical system from which positions of planets could be predicted in advance

put together past and current theories and observations in a thirteen-book treatise called

or The Mathematike Syntaxis
(The Mathematical Compilation)

excerpt from the Preface to Almagest (c. 150) by Claudius Ptolemy:

...And so, in general, we have to state:

that the heavens are spherical and move spherically;

that the earth, in figure, is sensibly spherical also when taken as a whole;

[that the earth] in position, lies right in the middle of the heavens, like a geometrical center;

[that the earth] in magnitude and distance, has the ratio of a point with respect to the sphere of the fixed stars, having itself no local motion at all.

And we shall go through each of these points briefly to bring them to mind.

Celestial Motions to be Explained

daily motion of fixed stars (from east to west)

superimposed eastward motion of sun, moon, and planets against background of fixed stars

Closer observation reveals variations on basic motions:

heavenly bodies (most notably the sun) periodically appear to speed up and slow down

planets occasionally appear to reverse their normal course [retrograde motion]

points where celestial equator and ecliptic intersect appear to drift slowly westward [precession of the equinoxes]

Direct motion of Mars is interrupted by retrograde motion from October 13, 1978 to May 29, 1979.

"Saving the Appearances"

According to Aristotle:

All celestial bodies, by their nature, move in perfect circles at constant speeds.

How can we account for what we see and still adhere to the laws of physics?

How can we "save the appearances"?

Ptolemy accounted for retrograde motion by introducing compound circular orbits.

A planet (Mars) moves at constant speed on an epicycle.

The center of the epicycle moves around the earth at a constant speed on the deferent circle.

The combined motion of a planet on its epicycle and deferent circles results in the appearance of retrograde motion as seen from earth.

____________________

To further refine his system, Ptolemy included two additional mathematical devices:

The first -- the eccentric circle -- was already in use by Ptolemy's time.

Planet moves on a circle, but that circle is not centered on the earth.

Planet moves at constant speed, but will appear to move faster when it is closer to earth, slower when it is farther away.

__________________________

The second mathematical device introduced by Ptolemy -- the equant point -- was his own invention.

The equant point (D) is located on the line connecting the earth (E) with the center of the planet's eccentric circle (F); DF = EF.

Center of the planet's epicycle (C) moves along the eccentric circle at a rate that would appear to be constant if viewed from the equant point.

Challenges Presented by Ptolemy's System

Why do planetary brightnesses change so much?

How can the sphere of the fixed stars spin so rapidly and not fly apart?

Which is really closer to Earth -- Venus or Mercury?

Are there additional mathematical devices that can improve the accuracy of astronomical prediction?

Is it possible to put all the individual planetary motions into one consistent and coherent system??

Go to:

History 135C Home Page

an excerpt from Republic by Plato (428-348 BCE)

an adapted excerpt from Plato's Timaeus

excerpts from On the Heavens by Aristotle (384-322 BCE)

an excerpt from the book Arrow of God by Nigerian author, Chinua Achebe (1930- ), describing the ritual observation of the new moon made by an aging Nigerian village priest in 1919

Weekly Readings	1	2	3	4	5	6	7	8	9	10
Lecture Notes	1	3	5	7	9	11	13	15	17	19
Lecture Notes	2	4	6	8	10	12	14	16	18	20