
University of California, Irvine
Instructor: Dr. Barbara J. Becker

|
|
| Re-examination of standard texts:
Claudius Ptolemy (2nd c CE)
or The Mathematike Syntaxis
The title of Ptolemy's treatise evolved to
or The Megiste Syntaxis
which the Arabs transliterated as al-Majisti. Gerard of Cremona translated Ptolemy's work into Latin from Arabic (1175) and al-Magisti became known as Almagest. |
Georg Peurbach (1426-1461) initiated the challenging task of translating
the Almagest directly from Greek into Latin. After Peurbach's
untimely death, the project was carried out by his pupil, Johannes Müller
of Königsberg (1436-1476), who was known by his latinized name, Johannes
de Regiomontanus (King's Mountain).

Frontispiece from The Epitome of Ptolemy (1496) shows Ptolemy (left) reading from the Almagest while Regiomontanus listens attentively (right) and points to the well-ordered celestial scheme that Ptolemy's great work describes. Gerard of Cremona's Latin translation of Almagest appeared in print in 1518. The first edition of Almagest in the original Greek was published in 1538. |
|
|
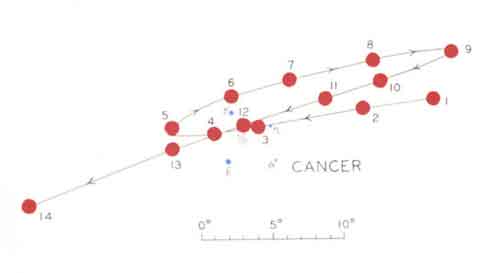
Direct motion of Mars is interrupted by retrograde motion from October 13, 1978 to May 29, 1979.
|
|
|
| According to Aristotle:
All celestial bodies, by their nature, move in perfect circles at constant speeds.
A planet (Mars) moves at constant speed on an epicycle. The center of the epicycle moves around the earth at a constant speed on the deferent circle. The combined motion of a planet on its epicycle and deferent circles results in the appearance of retrograde motion as seen from earth.
To further refine his system, Ptolemy included two additional mathematical devices: The first, the eccentric circle, was already in use by Ptolemy's time.
Planet moves on a circle, but that circle is not centered on the earth. Planet moves at constant speed, but will appear to move faster when it is closer to earth, slower when it is farther away. The second mathematical device introduced by Ptolemy, the equant point, was his own invention.
The equant point (D) is located on the line connecting the earth (E) with the center of the planet's eccentric circle (F); DF = EF. Center of the planet's epicycle (C) moves along the eccentric circle at a rate that would appear to be constant if viewed from the equant point. |
The Epitome of Ptolemy by Regiomontanus
(1496):
|
Minor annoying anomalies, or major unavoidable crisis?..... |
|
|
| Julian calendar year = 365.25 days, roughly equivalent to sidereal year (period of earth's revolution about the sun with respect to the stars). Keeps civil time.
Tropical year (period of earth's revolution about the sun with respect to the vernal equinox) = 365.242199 days. Keeps seasonal time. Tropical year is about 11 min 14 sec shorter than civil calendar year. Difference adds up to roughly one day every 130 years:
Church calendar conflict:
__________ Postscript on calendar reform: The Gregorian Calendar In 1582, Pope Gregory XIII decreed that in the Catholic Christian world, October 4, 1582 would be followed by October 15. He took this drastic action to bring the civil and seasonal calendars back into sync by realigning the vernal equinox with a part of the civil calendar that had been traditionally associated with the beginning of spring -- around the 20th of March. To prevent such disparities from building up in the future, he modified the rule for determining leap years. In the Julian calendar, every year that is divisible by four is a leap year. But that practice clearly inserts too many days. How many? Over a 400-year period, it will add three extra days. So every 400 years, three days will have to be eliminated to keep the civil calendar in seasonal alignment. How to choose those three days? Gregory decreed that century years would no longer be designated as leap years -- unless they were divisible by 400! |
|
Revolutionary, or Reactionary? |

|
|
| 1473 | born in Torun, Prussia (present-day Poland) |
| 1491 | enrolled at University of Cracow studied church law |
| 1496 | enrolled at University of Bologna studied Greek, philosophy, astronomy, medicine |
| 1500 | summoned to Rome for symposium on calendar reform |
| 1501 | enrolled at University of Padua; studied law and medicine |
| 1503 | returned to Torun; served as physician, cleric, scholar |
| 1514 | circulated treatise called Commentariolus (Little Commentary) among his friends |
|
Commentariolus (1514) by Nicholas Copernicus The planetary theories of Ptolemy and most other astronomers, although consistent with the numerical data, seemed likewise to present no small difficulty. For these theories were not adequate unless certain equants were also conceived ... a system of this sort seemed neither sufficiently absolute, nor sufficiently pleasing to the mind.Copernicus' assumptions in Commentariolus:
|
| 1538 | Georg Joachim Rheticus (1514-1575) arrived in Torun to study with Copernicus |
| 1540 | Rheticus published Narratio Prima (First Account) |
| 1541 | Rheticus encouraged Copernicus to prepare his treatise for publication |
| 1542 (May) | manuscript taken to printer in Nuremberg
Rheticus unable to oversee publication task taken over by Andreas Osiander |
| 1542 (Dec) | Copernicus suffers cerebral hemorrhage |
| 1543 (May) | publication is completed
Copernicus dies shortly afterwards |
|
|
|
Determining Relative Planetary Distances from the Sun in Copernicus'
Heliocentric System |
|
Distance of an inner planet (Venus) from the sun (sun-Earth distance
= 1 AU)
Distance of an outer planet (Mars) from the sun (sun-Earth distance = 1 AU) |
Distances from Planetary System Center |
|
Copernicus' system of the world from de Revolutionibus Orbium Coelestium (1543)
|
|
|
|
|
|
| The world system of Copernicus....
...or that of Ptolemy?
|
Why change? |
|