

Department of History
University of California, Irvine
Instructor: Dr. Barbara J. Becker
![]()
Lecture 2. From Chaos to Cosmos.
![]()
Early Sky Watchers -- The Greeks |
__________
|
||||||||||||
| Plato (429-348 BCE) |
Two worlds:
Mathematics (geometry) bridges these two worlds and makes the Ideal world accessible to human understanding through reason.
|
||||||||||||
Plato's Ideal Educational Plan |
||||||||||||
Quadrivium
 |
||||||||||||
Plato's "Likely Story" about the Structure and Substance of the Natural World |
||||||||||||
|
|
||||||||||||
Plato's Views on Time and the Heavens |
||||||||||||
Time came into being with the heavens.... As a result of this plan and purpose..., the sun and moon and the five planets ... came into being to define and preserve the measures of time.The earliest clocks and calendars were based on the natural rhythms of the Sun and the Moon. But what kind of time units can we measure using planetary motions? Can we identify cyclic patterns in the wanderings of the planets that can serve as markers for other useful units of time? How can the apparent complexity of planetary motions be described mathematically?--Plato, Timaeus The photographs below were taken during the conjunction of Venus, Mars, and Jupiter in June 1991. (Planets are said to be in conjunction when they share the same celestial longitude.) All three of these planets are moving against the background stars, but to simplify the complexities of their motion, I have fixed the position of Mars in each frame (it is the faint "star" in the upper left-hand corner). Venus (the brightest of the three bodies) can be seen moving
up toward Mars (upper left in the first frame). In the final frame, Venus has passed to the left of
Mars. Jupiter, meanwhile, moves down toward the bottom right
hand corner. In the final frame, the three planets form nearly a
straight line with Venus in the upper left corner, Jupiter in the lower
right corner, and Mars between them.
|
||||||||||||
Eudoxus of Cnidus (c. 400 - c. 347 BCE) |
||||||||||||
Eudoxus, a student of Plato, developed an ingenious mathematical system to bring some order to the complexities of planetary motion. Eudoxus treated each celestial body as a separate mathematical problem, but he tackled each of these problems in the same way. In his system, the motion of each planet (Mercury, Venus, Mars, Jupiter, and Saturn) is governed by a set of four nested concentric spheres -- one to govern its daily motion, one to govern its motion through the zodiac, and two to account for the looping appearance of its retrograde motion. The Sun and Moon were governed by three spheres each.
Simplified schematic of Eudoxus's concentric sphere model. The Earth (blue) sits in the center of the nested spheres that control the motion of the planet (red). The planet is shown embedded in a tilted sphere that carries it around the zodiac. This sphere is nested in a sphere that rotates daily on the polar axis of the fixed stars.
When all four spheres start rotating on their axes, the planet will appear to move along a complex path that resembles its observed motion across the sky. Eudoxus's model worked pretty well for Jupiter, Saturn, and Mercury, and less well for Venus and Mars. His younger contemporaries, like Callippus of Cyzicus and Aristotle, tried to improve the system's match with reality by adding more spheres. |
|
Aristotle, like Eudoxus, was a student of Plato. And, like all good students, he was critical of his teacher's ideas. Aristotle agreed that mathematics could serve as a model for good reasoning, but he questioned whether it was truly the sole path to scientific knowledge about the natural world. He acknowledged that mathematics is useful for gaining certain knowledge of the heavens, optics and perspective, but he found it to be limited when it comes to investigating many other natural phenomena. Living things, for example, do not adhere to rigid patterns of behavior. They require a new kind of reasoning, one based on what is probable, not just on what is certain. Aristotle regarded such probability-based reasoning as equally worthy a tool for the natural philosopher as reasoning that is based on mathematics. __________ Fundamentals of Aristotle's Natural Philosophy
All matter is made of two parts:
The tension and balance generated by opposing qualities is behind all change observed in terrestrial world. |
|||||||||||
Aristotle's Physics of the Terrestrial Realm |
|||||||||||
Each terrestrial element (earth, water, air, fire) has a natural place or state.
|
|||||||||||
Aristotle's Physics of the Celestial Realm |
|||||||||||
The celestial element (quintessence) has no opposing qualities.
|
|||||||||||
|
Aristotle was the tutor of Alexander the Great (356-323 BCE). After Alexander's death:
|
|
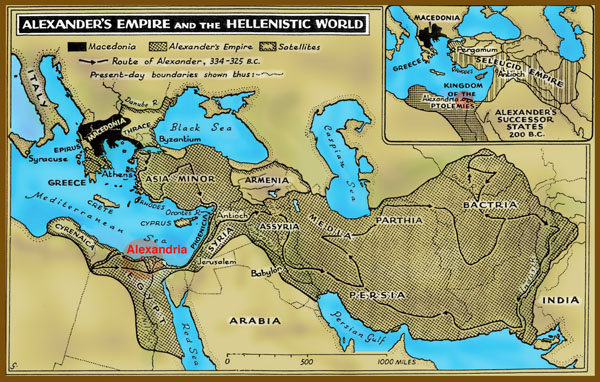
The Alexandrians
(Hellenistic Period -- Greek influence) |
||
| Euclid | 330-260 BCE | Mathematics
• wrote The Elements |
| Aristarchos | 310-230 | Astronomy • estimated size of Moon relative to Earth (see below) |
| Archimedes | 287-212 | Engineering |
| Eratosthenes | 276-195 | Math/Astronomy
• librarian at Alexandrian Museum • measured size of Earth (see below) |
| Hipparchus | 190-120 | Astronomy
• mapped the heavens • studied Babylonian records • discovered Earth's precession |
![]()
Aristarchos (c. 310 - c. 230 BCE) Measures the Moon |
|
|
Lunar eclipse, July 5-6, 1982 By measuring the amount of time it takes for the Moon to enter the Earth's shadow (about 1 hr) and then to cross the Earth's shadow (about 3 hours) during a lunar eclipse, Aristarchos was able to estimate that the Moon is about one-third the size of the Earth.
Aristarchos could not determine the absolute size of the Moon because no one had yet figured out a way to measure the size of the Earth! Also, Aristarchos knew that shadows of spheres are conical in shape, but he had no way to know how far away the Moon is when it cuts through Earth's shadow. To find out how much this affected his estimate, compare the size of the Earth and Moon using modern measures. |
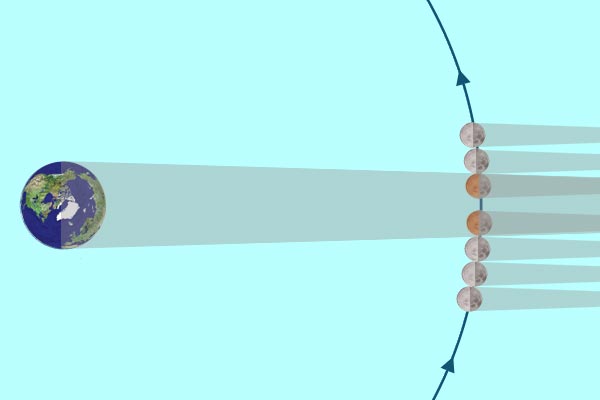
The Moon passing through the Earth's shadow during a lunar eclipse like the one in July 1982.
![]()
Eratosthenes (c. 276 - c. 195 BCE) Measures the Earth |
|
The world of Eratosthenes showing the location of the
cities of Alexandria and Syene.
Eratosthanes lived and worked in Alexandria. The city of Syene is located due south of Alexandria at a distance of 5000 Greek stades. In Syene, there is a very deep well. Eratosthenes had heard that very year on the day of the summer solstice, when the Sun is directly overhead at noon, a brilliant shaft of sunlight illuminates the water at the bottom of this well. ________________
Meanwhile, back in Alexandria, Eratosthenes observed and measured the length of a shadow cast at noon by the summer solstice Sun. Using geometry, he determined that the distance between Alexandria and Syene was one-fiftieth of the Earth's circumference.
|
|
The Alexandrians |
||
| Hero | fl. 62 CE | Optics
• studied reflection and refraction • constructed automated gadgets |
| Ptolemy | fl. 125 | Astronomy/Cartography
• wrote Almagest; The Geography |
| Galen | 131-201 | Medicine
• wrote On the Natural Faculties |
Claudius Ptolemy (c. 125 CE) |
Ptolemy was a Roman citizen of Greek descent who
pursued his mathematical interests at the great Museum in Alexandria, Egypt.
or The Mathematike Syntaxis
|
|
|
|
|
|
| According to Aristotle:
All celestial bodies, by their nature, move in perfect circles at constant speeds.
A planet (Mars) moves at constant speed on an epicycle. The center of the epicycle moves around the earth at a constant speed on the deferent circle. The combined motion of a planet on its epicycle and deferent circles results in the appearance of retrograde motion as seen from earth.
To further refine his system, Ptolemy included two additional mathematical devices: The first -- the eccentric circle -- was already in use by Ptolemy's time.
Planet moves on a circle, but that circle is not centered on the earth. Planet moves at constant speed, but will appear to move faster when it is closer to earth, slower when it is farther away. The second mathematical device introduced by Ptolemy -- the equant point -- was his own invention.
The equant point (D) is located on the line connecting the earth (E) with the center of the planet's eccentric circle (F); DF = EF. Center of the planet's epicycle (C) moves along the eccentric circle at a rate that would appear to be constant if viewed from the equant point. |
Challenges Presented by Ptolemy's System |
|
|